Return to Homepage

OVERHEAD CONTACT WIRES

Wire cross-sections

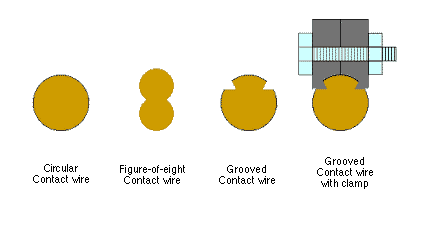
Ordinary electrical wire is circular in cross-section but this is difficult to suspend from overhead fittings in such a way that the contact device of the tramcar, pressing on the underside, does not foul the attachment points.

On the earliest tramways, the suspension 'ears' were soldered to the top and sides of the circular wire.

Soldered ears

Where soldering was undesirable, 'mechanical ears' were used but a circular wire restricted their area of grip. Wires of non-circular cross-section were developed so that mechanical attachment could be made to the upper side without being fouled by the contact device running on the lower side.

A mechanical ear on figure-of-eight wire

Electrical properties

The electrical resistance of overhead contact wire can be found from the following tables:

(The wire gauges follow historic tramway practice although present day manufacturers will often quote them in metric units.)

PROPERTIES OF HARD-DRAWN COPPER TROLLEY WIRE

Gauge	Diameter Inch	Sectional area		Resistance at 15.5°C		Weight		Breaking stress
		Sq. Inch	Sq. mm	Ohms Per Km	Ohms Per mile	Kg/Km	Lbs./mile	KN	Lbs.
0000000  S.W.G.	0.500	0.1964	126.7	0.1363	0.2193	1131	4005	40.80	9150
000000    S.W.G.	0.464	0.1691	109.1	0.1582	0.2546	972	3441	37.14	8330
0000  B&S	0.460	0.1661	107.2	0.1613	0.2596	955	3381	37.32	8370
00000      S.W.G.	0.432	0.1466	94.6	0.1825	0.2937	843	2983	32.95	7390
000   B&S	0.410	0.1320	85.2	0.1986	0.3196	759	2687	30.28	6790
0000        S.W.G.	0.400	0.1257	81.1	0.2129	0.3426	722	2557	28.76	6450
000         S.W.G.	0.372	0.1087	70.1	0.2461	0.3961	625	2212	24.97	5600
00    B&S	0.365	0.1046	67.5	0.2506	0.4033	601	2129	24.03	5390
00          S.W.G.	0.348	0.0951	61.6	0.2813	0.4527	547	1935	21.85	4900
0     B&S	0.325	0.0829	53.5	0.3219	0.5180	478	1692	19.04	4270
0            S.W.G.	0.324	0.0824	53.2	0.3245	0.5222	474	1678	18.95	4250

PROPERTIES OF SILICIUM BRONZE TROLLEY WIRE

Gauge	Diameter Inch	Sectional area		Resistance at 15.5°C		Weight		Breaking stress
		Sq. Inch	Sq. mm	Ohms Per Km	Ohms Per mile	Kg/Km	Lbs./mile	KN	Lbs.
0000000  S.W.G.	0.500	0.1964	126.7	0.1908	0.3071	1131	4005	62.16	13940
000000    S.W.G.	0.464	0.1691	109.1	0.2220	0.3574	972	3441	54.08	12130
00000      S.W.G.	0.432	0.1466	94.6	0.2562	0.4123	843	2983	47.58	10670
000   B&S	0.410	0.1320	85.2	0.2844	0.4577	759	2687	43.43	9740
0000        S.W.G.	0.400	0.1257	81.1	0.2989	0.4811	722	2557	41.87	9390
000         S.W.G.	0.372	0.1087	70.1	0.3455	0.5561	625	2212	36.34	8150
00    B&S	0.365	0.1046	67.5	0.3589	0.5777	601	2129	35.49	7960
00          S.W.G.	0.348	0.0951	61.6	0.3949	0.6356	547	1935	32.28	7240
0            S.W.G.	0.324	0.0824	53.2	0.4555	0.7330	474	1678	28.40	6370

Some sample calculations

Supposing a tramcar is at one end of a 1 Km length of 000 S.W.G. overhead copper wire, the sub station is supplying 750 volts to the other end. Calculate the voltage available to the tram when:

1)  The tram is switched off

From the above tables, the resistance of 1 Km of 000 S.W.G. copper wire is 0.2461 ohms
The current drawn through the wire = 0 Amps

Ohm's Law states that the voltage dropped equals  current  x  resistance

The voltage dropped in the wire in this case =  0  x  0.2461  = 0 volts
so the voltage available to the tram =  750 - 0  = 750 volts

2)  The tram accelerates hard and momentarily draws 200 Amps

Now the current through the wire is 200 Amps and its resistance is 0.2461 ohms

Ohms law says the voltage drop will be  200  x  0.2461  =  approx 50 volts

So the voltage available to the tram will be 750 - 50  = 700 volts

3)   The tram brakes and regenerates 100 amps

The voltage difference along the wire will be 100  x  0.2461  = approx 25 volts
but the current is now flowing from the tram to the sub-station end of the wire, the opposite direction from before. The voltage difference is now the other way around, it is a voltage gain.

The voltage at the tram will now be 750  +  25  = 775 volts

This is not magic, getting more than we started with. It shows that the tram is returning to the system, some of the energy it took when it accelerated

Return to Track and Vehicle Homepage